-
斯特林公式
编辑
- 斯特林公式
- Stirling's approximation
- 斯特灵公式
- n!≈√(2πn)·(n/e)^n
- 亚伯拉罕 棣莫弗
- 数学
- 数学
- 数学
目录
斯特林公式在理论和应用上都具有重要的价值,对于概率论的发展也有着重大的意义。在数学分析中,大多都是利用Г函数、级数和含参变量的积分等知识进行证明或推导,很为繁琐冗长。近年来,一些国内外学者利用概率论中的指数分布、泊松分布、χ²分布证之。
求n!的位数
利用斯特林(Stirling)公式的进行求解。下面是推导得到的公式:
res=(long)( (log10(sqrt(4.0*acos(0.0)*n)) + n*(log10(n)-log10(exp(1.0)))) + 1 );
当n=1的时候,上面的公式不适用,所以要单独处理n=1的情况!
这种方法速度很快就可以得到结果。
res=(long)( (log10(sqrt(4.0*acos(0.0)*n)) + n*(log10(n)-log10(exp(1.0)))) + 1 );
当n=1的时候,上面的公式不适用,所以要单独处理n=1的情况!
这种方法速度很快就可以得到结果。
或更精确的
或
令
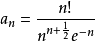
则


所以
 即
即
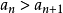 ,即单调递减,又由积分放缩法有
,即单调递减,又由积分放缩法有
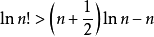
即
 ,即
,即
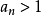
由单调有界定理
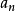 的极限存在,
的极限存在,
设
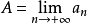
利用Wallis公式,



所以
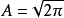
即
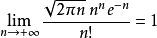
更加精确的近似公式为:
其中:
-
.
未经允许不得转载!斯特林公式(n的阶乘近似)