目标:
本章节你需要学习以下内容:
- 查找轮廓的不同特征,如面积,周长,质心,边界框等
1. 矩
图像的矩可帮助你计算某些特征,如对象的质心,对象的面积等特征。具体定义可以查看图像的矩的维基百科页面
函数cv.moments()给出了计算的所有矩值的字典。
import numpy as np
import cv2 as cv
img = cv.imread('star.jpg',0)
ret,thresh = cv.threshold(img,127,255,0)
contours,hierarchy = cv.findContours(thresh, 1, 2)
cnt = contours[0]
M = cv.moments(cnt)
print( M )
从这一刻起,你可以提取有用的数据,如面积,质心等。质心由关系给出,和 。这可以按如下方式完成:
cx = int(M['m10']/M['m00'])
cy = int(M['m01']/M['m00'])
2. 轮廓面积
轮廓区域由函数cv.contourArea()或时刻M[‘m00’]给出。
area = cv.contourArea(cnt)
3. 轮廓周长
轮廓周长也被称为弧长。可以使用cv.arcLength()函数找到它。第二个参数指定形状是闭合轮廓(如果传递为True),还是仅仅是曲线。
perimeter = cv.arcLength(cnt,True)
4. 轮廓近似
它根据我们指定的精度将轮廓形状近似为具有较少顶点数的另一个形状。它是Douglas-Peucker算法的一种实现方式。
要理解这一点,可以假设你试图在图像中找到一个正方形,但是由于图像中的一些问题,你没有得到一个完美的正方形,而是一个“坏形状”(如下图第一张图所示)。现在你可以使用此功能来近似形状。在这里,第二个参数称为epsilon,它是从轮廓到近似轮廓的最大距离。这是一个准确度参数。需要选择适当的epsilon才能获得正确的输出。
epsilon = 0.1*cv.arcLength(cnt,True)
approx = cv.approxPolyDP(cnt,epsilon,True)
下面,在第二幅图像中,绿线表示epsilon=弧长的10%的近似曲线。第三幅图像显示相同的epsilon=弧长的1%。第三个参数指定曲线是否关闭。
5. 凸包
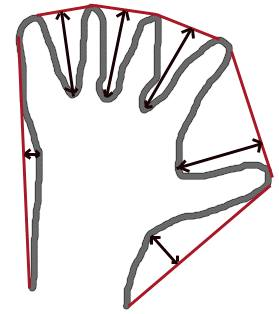
凸包看起来类似于轮廓近似,但它不是(两者在某些情况下可能提供相同的结果)。这里,cv.convexHull()函数检查曲线的凸性缺陷并进行修正。一般而言,凸曲线是总是凸出或至少平坦的曲线。如果它在内部膨胀,则称为凸性缺陷。例如,检查下面的手形图像。红线表示手的凸包。双面箭头标记显示凸起缺陷,即船体与轮廓的局部最大偏差。
下面我们要讨论它的一些语法:
hull = cv.convexHull(points[, hull[, clockwise[, returnPoints]]
参数详情:
- points:是我们传入的轮廓。
- hull:是输出,通常我们忽略它。
- clocwise:方向标志。如果为True,则输出凸包顺时针方向。否则,它逆时针方向。
- returnPoints:默认为True。然后它返回凸包点的坐标。如果为False,则返回与凸包点对应的轮廓点的索引。
因此,为了获得如上图所示的凸包,以下就足够了:
hull = cv.convexHull(cnt)
但是如果你想找到凸性缺陷,你需要传递returnPoints = False。为了理解它,我们将采用上面的矩形图像。首先,我发现它的轮廓为cnt。现在我发现它的凸包有returnPoints = True,我得到以下值:[[234 202],[51 202],[51 79],[234 79]]这四个角落 矩形点。 现在如果对returnPoints = False做同样的事情,我得到以下结果:[[129],[67],[0],[142]]。 这些是轮廓中相应点的索引。例如,检查第一个值:cnt [129] = [[234,202]],它与第一个结果相同(对于其他结果,依此类推)。
当我们讨论凸性缺陷时,你会再次看到它。
6. 检查凸性
函数cv.isContourConvex()可以检查曲线是否凸的,它只返回True或False,没有什么理解上的问题。
k = cv.isContourConvex(cnt)
7. 边界矩形
有两种类型的边界矩形。
7.a.直边矩形
它是一个直的矩形,它不考虑对象的旋转。因此,边界矩形的面积不是最小的。它由函数cv.boundingRect()找到。
设(x,y)为矩形的左上角坐标,(w,h)为宽度和高度。
x,y,w,h = cv.boundingRect(cnt)
cv.rectangle(img,(x,y),(x+w,y+h),(0,255,0),2)
7.b.旋转矩形
这里,以最小面积绘制边界矩形,因此它也考虑旋转。使用的函数是cv.minAreaRect()。它返回一个Box2D结构,其中包含以下detals - (center(x,y),(width,height),rotation of rotation)。但要画这个矩形,我们需要矩形的4个角。它是由函数cv.boxPoints()获得的
rect = cv.minAreaRect(cnt)
box = cv.boxPoints(rect)
box = np.int0(box)
cv.drawContours(img,[box],0,(0,0,255),2)
两个矩形都显示在单个图像中。绿色矩形显示正常的边界矩形。红色矩形是旋转的矩形。
8. 最小外接圈
接下来,我们使用函数cv.minEnclosingCircle()找到对象的外接圆。它是一个完全覆盖物体的圆圈,面积最小。
(x,y),radius = cv.minEnclosingCircle(cnt)
center = (int(x),int(y))
radius = int(radius)
cv.circle(img,center,radius,(0,255,0),2)
9. 椭圆拟合
接下来是将椭圆拟合到一个对象上。它返回刻有椭圆的旋转矩形。
ellipse = cv.fitEllipse(cnt)
cv.ellipse(img,ellipse,(0,255,0),2)
10. 拟合一条线
类似地,我们可以在一组点上拟合一条线。下图包含一组白点。 我们可以近似直线。
rows,cols = img.shape[:2]
[vx,vy,x,y] = cv.fitLine(cnt, cv.DIST_L2,0,0.01,0.01)
lefty = int((-x*vy/vx) + y)
righty = int(((cols-x)*vy/vx)+y)
cv.line(img,(cols-1,righty),(0,lefty),(0,255,0),2)
未经允许不得转载!OpenCV-python中的图像处理-轮廓特征